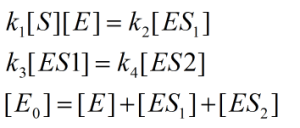Home»Math Guides»Michaelis Menten Kinetics, Fast Equilibrium Assumption, Example 1
Michaelis Menten Kinetics (Fast Equilibrium Assumption) Solved Example Problem 1
We have two different assumptions when finding the product formation rate in Michaelis-Menten kinetics, either the fast equilibrium approach or the pesudo steady state approach.
Let’s solve a series of biochemical reactions using the fast equilibrium assumption.
Here, [E\(_0\)] represents the initial concentration of the enzyme, [S] represents concentration of the substrate, and [ES\(_1\)], [ES\(_2\)] represent concentrations of the enzyme-substrate complexes.
Find the product formation rate of: ![]()
Let’s use the equilibrium assumption first.
Do a mass balance on the left reaction, a mass balance on the right reaction, and a mass balance on all enzyme-containing chemicals, and we obtain (remember, fast equilibrium assumption):
Remember, when we find the product formation rate, we want it to be a function of only [S] and [E\(_0\)], we don’t want any of the enzyme-substrate intermediates to appear in our equation.
Now substitute and rearrange to acquire:
\[[E{S_1}] = \frac{{{k_1}}}{{{k_2}}}[S][E]\]
\[[E{S_1}] = \frac{{{k_4}}}{{{k_3}}}[E{S_2}]\]
And substitute into the equation for [E].
\[[E] = \frac{{{k_2}{k_4}}}{{{k_1}{k_3}}} \cdot \frac{{[E{S_2}]}}{{[S]}}\]
Plug these into the equation for [E\(_0\)] and factor out the [ES\(_2\)] term.
\[[{E_0}] = \left[ {\frac{{{k_2}{k_4} + {k_1}{k_4}[S] + {k_1}{k_3}[S]}}{{{k_1}{k_3}[S]}}} \right][E{S_2}]\]
Now isolate for [ES\(_2\)] by rearranging.
\[[E{S_2}] = \frac{{{k_1}{k_3}[{E_0}][S]}}{{{k_2}{k_4} + {k_1}{k_4}[S] + {k_1}{k_3}[S]}}\]
The product formation rate (or reaction velocity) is:
\[\frac{{dP}}{{dt}} = \nu = {k_5}[E{S_2}]\]
Now substitute in what we found for [ES\(_2\)] earlier.
\[\nu = \frac{{{k_1}{k_3}{k_5}[{E_0}][S]}}{{{k_2}{k_4} + {k_1}{k_4}[S] + {k_1}{k_3}[S]}}\]
Now, if you carefully do algebra, you can show this follows Michaelis-Menten kinetics.
Divide the numerator and denominator terms by k\(_1\)k\(_3\).
\[\nu = \frac{{{k_5}[{E_0}][S]}}{{\frac{{{k_2}{k_4}}}{{{k_1}{k_3}}} + \frac{{{k_1}{k_4}}}{{{k_1}{k_3}}}[S] + \frac{{{k_1}{k_3}}}{{{k_1}{k_3}}}[S]}}\]
\[\nu = \frac{{{k_5}[{E_0}][S]}}{{\frac{{{k_2}{k_4}}}{{{k_1}{k_3}}} + \frac{{{k_4}}}{{{k_3}}}[S] + [S]}}\]
\[\nu = \frac{{{V_m}[S]}}{{{K_{m2}}({K_{m1}} + [S]) + [S]}}\]
Where \({K_{m1}} = \frac{{{k_2}}}{{{k_1}}}\) and \({K_{m2}} = \frac{{{k_4}}}{{{k_3}}}\)