Home»Math Guides»Double Iterated Integrals using Polar Coordinates (circular region of integration) example 1
Examples of Double Integrals in Polar Coordinates (Example 1)
How to use polar coordinates transformation to solve double integrals with circlular regions of integration
We want to find the value of the following definite integral by converting the double integral into polar coordinates.
How would you know to use polar coordinates if the question only said “Find the integral”?
Well, if you see equations in the integral boundaries that resemble a circle or ellipsis (squared variable terms), then generally you know you need to use polar coordinates to simplify and solve the integral.
Compared to integral boundaries that are just numbers, polar coordinate integral problems look very distinctive.
Example Problem: Solve the integral \(\int_{ – 3}^3 {} \int_0^{\sqrt {9 – {x^2}} } {\sin ({x^2} + {y^2})dydx} \)
The first thing to do is change the coordinates to polar coordinates and determine new lower and upper integral bounds.
In general, use the substitutions listed below, which you should memorize, though they may be provided and on a cheat sheet.
\[\begin{array}{l}x = r\cos (\theta )\\y = r\sin (\theta )\\{r^2} = {x^2} + {y^2}\\dxdy = rdrd\theta \end{array}\]
Also, you need to make the integral bounds, which will be in terms of r and theta.
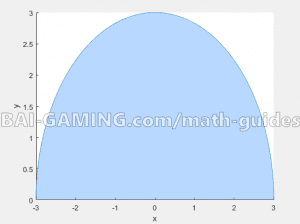
The best thing to do is to do a little sketch of what the plot looks like in the x and y coordinates.
Notice that x is from -3 to 3 in that integral, you know quadrants 1 and 2 have something in the plot.
But the y integral goes from 0 to the root of 9-x^2, which means nothing exists below the y axis because the lowest value is y = 0, you can’t go lower than the lower boundary which is told to be 0.
As well, the upper bound on y is that equation, which is just a circle of radius 3 (you square root the 9).
Technically the root of 9 can be positive or negative 3, BUT the lower boundary is told to be y = 0, so you know the upper boundary must be positive 3.
Basically, a sketch of the region of integration in x and y is just a hemi-circle existing only above the y-axis.

If you want to plot a sketch of the region of integration above in MATLAB, use the following code (the circle goes from 0 to pi, radius of 3, and no shifting transformation, feel free to modify and use for other types of circles):
hold on
theta = 0:pi/100:pi
x = 3 * cos(theta) + 0;
y = 3 * sin(theta) + 0;
h = plot(x, y);
xlabel('x')
ylabel('y')
hold offWe need to take these x and y coordinates and somehow get new integral boundaries.
We know x and y coordinate region of integration is over a hemi-circle over the y axis. Remember that we have \({\sqrt {9 – {x^2}} }\), which looks like an equation for a circle.
All you need to do is square root the 9 to get 3. So basically this hemicircle has a maximum radius of 3.
And the hemicircle starts at radius 0 as well. So the bounds on r is from 0 to 3. Easy!
For theta, you need to see how far the circle you sketched goes.
It’s a hemicircle above the y-axis, and basically for each quadrant you go through you need to add \(\frac{\pi }{2}\)
This hemicircle exists above the y-axis, so it’s just going to the second quadrant, so theta goes from 0 to \(pi \).
Remember, you start at the positive x axis, and you move counter-clockwise when counting quadrants.
We also need to substitute \({r^2} = {x^2} + {y^2}\) into the argument of the sine, and also add an extra “r” when we transform to polar coordinates.
Substituting all of this into the original integral, we get:
\[\int_0^\pi {} \int_0^3 {\sin ({r^2})rdrd\theta } \]
To solve this, we need to use regular substitution. Let \(u = {r^2}\), then \(du = 2rdr\)
Or, \(rdr = \frac{{du}}{2}\)
Doing this changes the integral boundaries as well, so we need to square the r boundaries.
Substituting these in, \(\int_0^\pi {} \int_{{0^2}}^{{3^2}} {\frac{1}{2}\sin (u)dud\theta } \)
And we solve the inner integral we get \(\int_0^\pi {\frac{1}{2}} \left( {1 – \cos (9)} \right)d\theta \)
You can simplify sines and cosines if you have a term with pi in them, but cos(9) can’t really be simplified.
Just work through the final integral again, which is just multiplying it by theta and evaluating it at both integral boundaries.
You will end up with the following as your final expression.
\[\frac{{\pi \left( {1 – \cos (9)} \right)}}{2}\]
Try another example problem where you solve another double integral using polar coordinates!