Home»Math Guides»Double inclined plane with friction, 2 boxes physics problem example
How to solve for tension and acceleration in double inclined plane with friction, 2 boxes
If you haven’t, review the 2-boxes on an inclined slope problem we solved previously here, it will go over the equations in more detail.
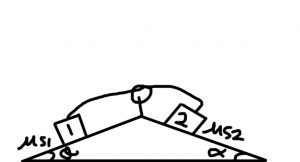
Consider the following diagram:
Example: Masses 1 and 2 are on a double inclined plane, with angels of theta and alpha to the horizontal and static coefficients acting on each of the blocks.
The trick is that there are different ways that the system can move, depending on high angle is higher and which block weighs more.
Case 1: Block 1 rises to the right and block 2 slides down to the right
Case 2: Block 1 falls to the left and block 2 rises to the left
Case 3: Acceleration is 0 and there is no movement.
The issue is that you might not necessarily know whether your system is case 1 or 2. But you need to know this because friction needs to act opposite to the direction of movement. Usually you aren’t asked for case 3, but it is possible for that to happen as a “trick question”.
You will formulate two equations with two unknowns to solve for, force of tension in the string and the common acceleration.
So you need to guess which case it is, and see if you were correct in your guess. BUT, if you wrong in your guess, you need to redo the question because all your frictions will be in the wrong direction, meaning your calculation will be wrong. So be very careful.
Now, there is a formula you can use to determine which case you have, we can prove this later:
Case 1: \({m_2}\sin (\theta ) – {m_1}\sin (\alpha ) > {\mu _{S1}}{m_1}\cos (\theta ) + {\mu _{S2}}{m_2}\cos (\alpha )\)
Case 2: \({m_1}\sin (\theta ) – {m_2}\sin (\alpha ) > {\mu _{S1}}{m_1}\cos (\theta ) + {\mu _{S2}}{m_2}\cos (\alpha )\)
Case 3: \(\left| {{m_1}\sin (\theta ) – {m_2}\sin (\alpha )} \right| \le \left| {{\mu _{S1}}{m_1}\cos (\theta ) + {\mu _{S2}}{m_2}\cos (\alpha )} \right|\)
We will show an example of each case, but we will exaggerate the cases to make it easier.
Example: Solve for tension and acceleration, given mass 1 = 100 kg, mass 2 = 5 kg, theta = 45 degrees, alpha = 10 degrees, static coefficient of friction 1 = 0.10, static coefficient of friction 2 = 0.35.
Here, we exaggerated that the system was moving to the left, left is positive and right is negative. Make all the equations:
\[{F_{N1}} = {m_1}g\cos (\theta )\]
\[{F_{N2}} = {m_2}g\cos (\alpha )\]
\[{F_{friction1}} = {\mu _{S1}}{m_1}g\cos (\theta )\]
\[{F_{friction2}} = {\mu _{S2}}{m_2}g\cos (\alpha )\]
\[{m_1}a = {m_1}g\sin (\theta ) – {\mu _{S1}}{m_1}g\cos (\theta ) – T\]
\[{m_2}a = – {m_2}g\sin (\alpha ) – {\mu _{S2}}{m_2}g\cos (\alpha ) + T\]
Do a bit of algebra and solve for acceleration (isolate for T and substitute in) to get:
\[a = \frac{g}{{{m_1} + {m_2}}}\left( {{m_1}\sin (\theta ) – {m_2}\sin (\alpha ) – {\mu _{S1}}{m_1}\cos (\theta ) – {\mu _{S2}}{m_2}\cos (\alpha )} \right)\]
There we go, that’s how we derived one of the cases equations earlier (the terms in the numerator need to be greater than the static friction cosine terms)!
The only tricky concept is to remember how the component of gravity (those sine terms) from the ramp works on the blocks, it helps push block 1 left, but it pushes block 2 right. The entire system moves to the left, so the friction forces are always to the right. Tension pulls block 1 right, but pulls block 2 left.
You can plug in the given values to the equation above and solve the question:
Acceleration is roughly 5.70 m/s2 and tension is roughly 53.94 N.
Example: See the illustrated diagram from earlier. Solve for tension and acceleration, given mass 1 = 10 kg, mass 2 = 85 kg, theta = 5 degrees, alpha = 50 degrees, static coefficient of friction 1 = 0.05, static coefficient of friction 2 = 0.2.
Now the system moves to the right. Make all the equations again, but now let’s say right is positive and left is negative.
\[{m_1}a = – {m_1}g\sin (\theta ) – {\mu _{S1}}{m_1}g\cos (\theta ) + T\]
\[{m_2}a = {m_2}g\sin (\alpha ) – {\mu _{S2}}{m_2}g\cos (\alpha ) – T\]
\[a = \frac{g}{{{m_1} + {m_2}}}\left( {{m_2}\sin (\alpha ) – {m_1}\sin (\theta ) – {\mu _{S1}}{m_1}\cos (\theta ) – {\mu _{S2}}{m_2}\cos (\alpha )} \right)\]
We derived another case equation, see that the numerator terms with sines must dominate over the static friction terms that have cosines.
Now substitute in your values and solve.
Acceleration is roughly 5.45 m/s2 and tension is roughly 67.97 N.
Let’s now try a stranger case, where we solve for variables when the system is stationary.
Example: See the illustrated diagram from earlier. The system remains at rest. Theta = 5 degrees and alpha = 8 degrees, static coefficient of friction 1 = 0.6, static coefficient of friction 2 = 0.5. The tension in the rope is 80 N. What are the masses of the two blocks?
Now we set a to be zero.
Use the above equations, setting a to be zero.
\[0 = T – {m_1}g\left( {{\mu _{S1}}\cos (\theta ) + \sin (\theta )} \right)\]
\[0 = – T + {m_2}g\left( {\sin (\alpha ) + {\mu _{S2}}\cos (\alpha )} \right)\]
Solving, mass 1 is approximately 11.91 kg and mass 2 is approximately 12.86 kg.
You can check the equation listed earlier to see if this is truly a stationary case:
\[\left| {{m_1}\sin (\theta ) – {m_2}\sin (\alpha )} \right| \le \left| {{\mu _{S1}}{m_1}\cos (\theta ) + {\mu _{S2}}{m_2}\cos (\alpha )} \right|\]
Substitute the masses into the equation above,
Is 0.75 lower than 13.48?
Yes, so the blocks are indeed stationary.
Technically, there are many more combinations of masses that will satisfy the equations too.
Try a physics problem with multiple pulleys involving the “conservation of string” concept