Home»Math Guides»Stacked Blocks Physics Problems
How to find equations for forces of friction, gravity, normal in stacked box problems
How exactly do you handle physics problems where you have multiple boxes stacked on top of each other, and you need to find all the equations and forces in the system? You just need to handle it step-by-step.
Please consider making a contribution to me by using Paypal: https://paypal.me/BAIZEGAMING
Consider buying us a coffee for our efforts –
BTC – 33iDpHvVwwcMyxhrv83rL75TXpmgBd72Xv
2 Stacked Boxes Worked-out Example Problem
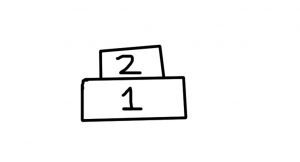
Example: Let’s consider the diagram above that shows two stacked boxes or masses. Mass 1 has a mass of 15 kg, and mass 2 has a mass of 5 kg. There is a floor beneath mass 1, with static and kinetic friction coefficients of 0.3 and 0.2, respectively. The static and kinetic friction coefficients between box 1 and 2 are 0.4 and 0.32, respectively.
Question: What is the maximum force you can apply to mass 1 before the two masses begin to move together?
When they’re about to move together you can treat them as a single object. Use the static friction coefficient between box 1 and the floor, don’t confuse all the information you’ve been given!
For the force due to friction:
\[{F_F} = {\mu _S}{F_N}\]
The normal force of the bottom box is the weights of all of the boxes.
\[{F_F} = (0.3)(15 + 5)(9.81)\]
\[{F_F} = 58.86N\]
And remember that m*a = sum of all forces
\[ma = {F_{applied}} – {F_F}\]
Now, “just begin to move” means that acceleration is 0.
\[{F_{applied}} = {F_F}\]
\[{F_{applied}} = 58.86N\]
So the maximum force you could apply before the system would begin to move is roughly 58.86 N.
Question: What is the maximum force you can apply to the bottom block without causing the top box to begin to slide away the bottom block? (Sometimes they will word this as, “how much force do you need to use the begin to push out the lower block”, it’s just the same question type, learn to recognize how they can word questions in various ways!)
The trick to this is that for the top box to not begin to start sliding, the top box acceleration must be equal to that for the bottom box acceleration.
You can do a vertical force balance on the second box, remember that it sums to 0 because the top box will not “fly off” the bottom box:
\[{F_N} – {m_2}g = m{a_y} = 0\]
\[{F_N} = {m_2}g\]
\[{F_N} = (5)(9.81)\]
\[{F_N} = 49.05N\]
The force on the top box can be equal to the frictional force on top without slipping. Use the static friction coefficient between box 1 and 2 now!
\[{F_F} = {\mu _S}{F_N}\]
\[{F_F} = (0.4)(49.05N)\]
\[{F_F} = 19.62N\]
\[{m_2}a = {F_F} = 19.62\]
\[a = \frac{{19.62}}{5}\]
\[a = 3.92\]
So the top box can have a maximum acceleration of 3.92 m/s2, which will also be the acceleration for the lower box as well so that the “no slipping” condition is met. Now we make equations for the bottom box:
There is another trick when doing a bottom box force balance! You have friction from the floor, but you also have the friction between boxes 1 and 2 acting on box 1!
Pretend that you shove box 1 to the right.
Well it will have a regular kinetic friction force to the left, which is the opposite of the direction of motion.
If box 1 is shoved to the right, box 2 on top will move to the left, in the opposite direction of box 1.
But that means that box 2 will have a friction force to the right.
Now, when there’s a friction between two boxes, the friction force term will appear in both boxes, in opposite directions! So if box 2 has a friction force to the right, box 1 has a friction force to the left. This is a static force because it is before box 2 begins to slip, or move.
For the vertical force balance on box 1 (note, now use the kinetic friction between box 1 and the floor, and use static friction for the friction between box 1 and box 2):
\[{F_N} – ({m_1} + {m_2})g = 0\]
\[{F_N} = (15 + 5)g = 0\]
\[{F_{F,floor}} = (0.2)(15 + 5)(9.81)\]
\[{F_{F,floor}} = 39.24N\]
Friction between the boxes is the same magnitude as it was found in the top box:
\[{F_{F,betweenboxes}} = 19.62N\]
Now sum all of the horizontal forces for the bottom block, remember that the acceleration matches from the top block for no slipping:
\[{F_{applied}} – {F_{F,floor}} – {F_{F,betweenboxes}} = {m_1}a\]
\[{F_{applied}} = (15)(3.92) + 39.24 + 19.62\]
You get 117.67 N. This is the maximum amount of force you can apply to the bottom block without causing the top block to begin to slip.
Question: A force of 150 N is now applied to the bottom box. What is the acceleration of each box?
Now 150 > 117, so the top box will start slipping, and the boxes will each have their own acceleration. Now you’ll be using the kinetic friction coefficient for the top box.
For the top box:
\[{F_{F,betweenboxes}} = {\mu _k}{F_{N,top}} = {\mu _k}{m_2}g\]
\[{F_{F,betweenboxes}} = (0.32)(5)(9.81)\]
\[{F_{F,betweenboxes}} = 15.70\]
\[15.70 = {m_2}{a_2}\]
\[{a_2} = \frac{{15.70}}{5} = 3.14\]
The force of friction between the floor and the bottom box is the same as before:
\[{F_{F,floor}} = (0.2)(15 + 5)(9.81)\]
\[{F_{F,floor}} = 39.24N\]
Do a horizontal force balance on the bottom box:
\[{F_{applied}} – {F_{F,floor}} – {F_{F,betweenboxes}} = {m_1}{a_1}\]
\[150 – 39.24 – 15.70 = (15){a_1}\]
We get a1 = 6.33 m/s2, and we found a2 earlier as 3.14 m/s2, which are the accelerations of the bottom box and top box, respectively.
Question: The top box has a negligible length, and that the bottom box has a length of 8 m. How long would it take the top box to fall off the bottom box?
Just find the difference between the accelerations and equate it to the distance of 8, but use the proper kinematic equations which involve 1/2 terms and t squared terms, remember to take the positive t value:
\[\frac{1}{2}(6.33 – 3.14){t^2} = 8\]
Solving, roughly t = 2.24 seconds. After this time the top block cannot keep up with the bottom block and falls off the bottom block.
3 Stacked Boxes Worked-out Example Problem
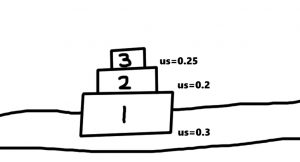
Example: Now consider a system of three vertically stacked boxes in the diagram below:
Consider boxes 1, 2 and 3 stacked as shown above, the masses are 9 kg, 6 kg, and 3 kg, respectively. The coefficients of static friction are 0.3 between the floor and box 1, 0.2 between boxes 1 and 2, and 0.25 between boxes 2 and 3.
Question: What are the accelerations of the boxes when 10 N of force is applied to box 2?
\[{F_F} = {\mu _S}{F_N}\]
\[{F_F} = (0.2)(3 + 6)(9.81)\]
\[{F_F} = 17.66N\]
And also add the force of friction from the top box, (0.25)(3)(9.81)
You will see these static friction forces are more than 10 N of applied force.
Since the friction force exceeds applied force, the boxes will move together with the same acceleration, so you apply the 10 N to all masses at once. So you can treat it as all 3 moving together.
\[10 = (3 + 6 + 9)a\]
\[a = 0.56\]
So the acceleration of all three boxes would be 0.56 \(m/{s^2}\) .
Question: What are the accelerations of the boxes when 30 N of force is applied to box 2?
Now this applied force exceeds the frictional force holding box 2.
You can find the net acceleration of the second box using the net force. But remember that the top block will have a friction force as well that applies to box 2. Now each block will have a different acceleration value, be careful!
\[{F_F} = (0.25)(3)(9.81)\]
\[{F_F} = 7.36N\]
\[30 – 17.66 – 7.36 = 4.98N\]
\[{a_2} = \frac{{4.98}}{6} = 0.83\]
Block 2’s acceleration is roughly 0.83 \(m/{s^2}\).
So, notice how we had friction forces 17.66 N and 7.36 N acting on block 2? Well each of these act on block 3 and on block 1, respectively.
This is Newton’s Third Law for friction, the friction will have equal and opposite directions between interfaces. In this case, the interfaces are the surfaces between the boxes.
There are no other horizontal forces for box 3.
For box 3, the top box:
\[{a_3} = \frac{{7.36}}{3} = 2.45\]
For box 1, the bottom box:
\[{F_F} = (0.3)(3 + 6 + 9)(9.81)\]
\[{F_F} = 52.97N\]
The frictional force from block 2 that goes to block 1 is only 17.66 N and is lower than the value above. So block 1 doesn’t move and has an acceleration of 0. If the bottom block didn’t have any friction, it would’ve been accelerating too.
Just remember that in these kinds of problems that the friction force term will always be paired in the opposite direction at the interface between blocks. The exception is the block on the floor, that will have its own friction without a pair because the floor doesn’t do anything. But if you have a block on top of that block, its friction will be paired with the block below it.
Say right is positive and left is negative. Say you have 2 blocks stacked – you push the bottom block to the right, and that block will have friction to the left, well, the upper block will have its own friction to the right which also carries back down to the bottom block. In the end, our bottom block will have ma = positive the force you pushed it, minus its own friction, minus the friction from the upper block. The upper block will have ma = positive its own friction.
If you pushed the upper block to the right, then it has friction to the left. The lower block will have friction to the right, which will need to exceed the bottom block static friction if the bottom block is to move. If it does exceed, then the bottom block is friction from the upper block minus its own friction.
Try a physics problem with multiple pulleys involving the “conservation of string” concept